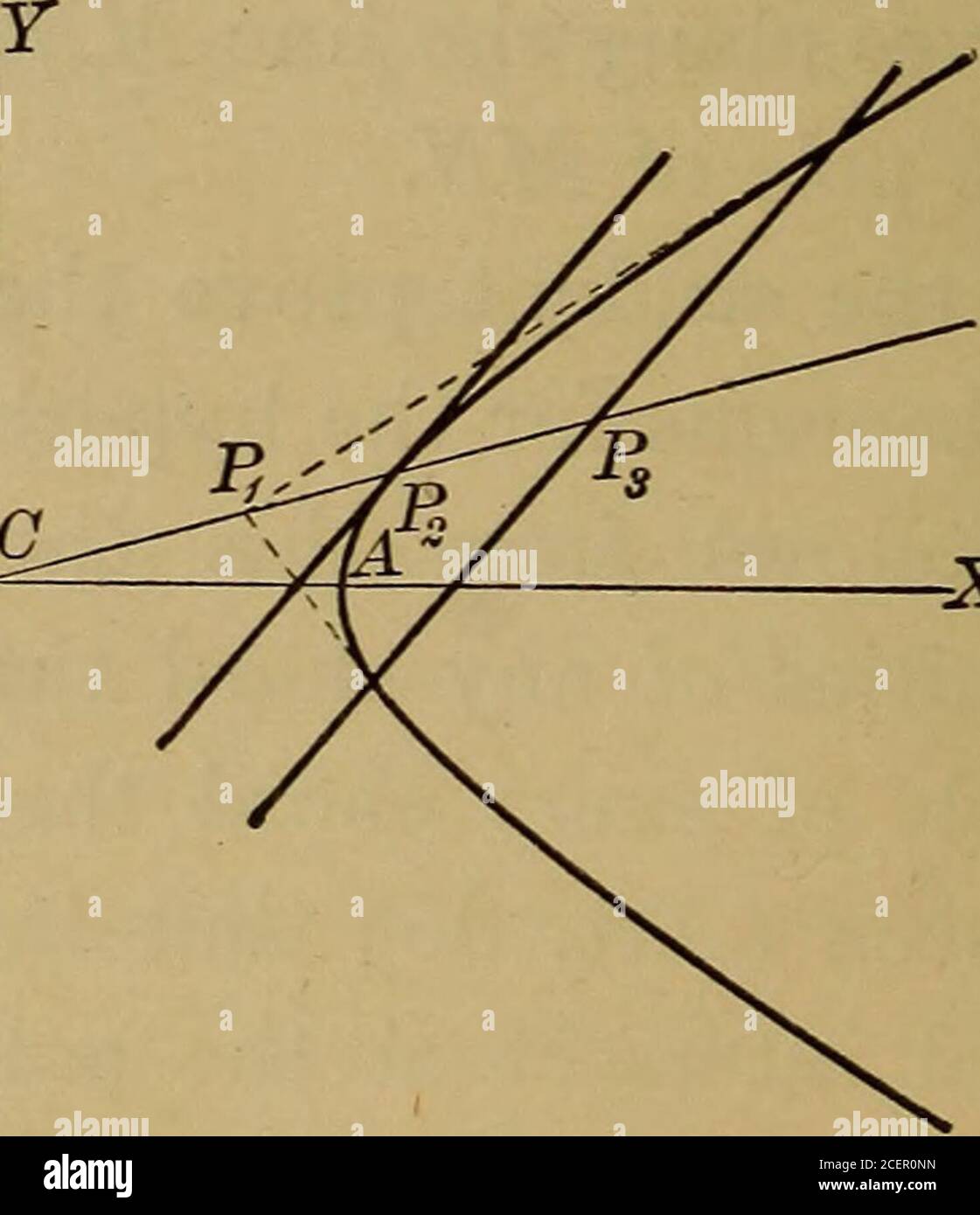
. Ebene und feste analytische Geometrie; ein elementares Lehrbuch. – X 9 Abb. 88. Ch. XII, Pole UND POLARE 161 Lasst die Koordinaten des Punktes P2, an dem CPX die Hyperbel schneidet, sein (xvy^). Dann ist die Gleichung der Tangente 2 b2x2x – a2y2y = a2b und die Gleichung der Polarität von P1 isb2xxx – A2yxy = a2b2.Da aber px und P2 durch den Ursprung auf derselben Linie liegen, -i = -?, und diese Linien offensichtlich parallel sind, soll der Student den gleichen Satz für die Ellipse nachweisen.3. Das Polar eines beliebigen Punktes px in Bezug auf eine Parabel ist parallel zur Tangente am Punkt, wo ein DurchmesserP1 die Parabel schneidet

. Ebene und feste analytische Geometrie; ein elementares Lehrbuch. – X 9 Abb. 88. Ch. XII, Pole UND POLARE 161 Lasst die Koordinaten des Punktes P2, an dem CPX die Hyperbel schneidet, sein (xvy^). Dann ist die Gleichung der Tangente 2 b2x2x – a2y2y = a2b und die Gleichung der Polarität von P1 isb2xxx – A2yxy = a2b2.Da aber px und P2 durch den Ursprung auf derselben Linie liegen, -i = -?, und diese Linien offensichtlich parallel sind, soll der Student den gleichen Satz für die Ellipse nachweisen.3. Das Polar eines beliebigen Punktes px in Bezug auf eine Parabel ist parallel zur Tangente am Punkt, wo ein DurchmesserP1 die Parabel schneidet Stockfoto

RMID:2CER0NN

Bilddetails

Bildanbieter:

Reading Room 2020

Bild-ID:

2CER0NN

Dateigröße:

7,1 MB (138,1 KB Komprimierter Download)

Freigaben (Releases):

Model - nein | Eigentum - neinBenötige ich eine Freigabe?

Format:

1468 x 1702 px | 24,9 x 28,8 cm | 9,8 x 11,3 inches | 150dpi

Weitere Informationen:

Dieses Bild ist ein gemeinfreies Bild. Dies bedeutet, dass entweder das Urheberrecht dafür abgelaufen ist oder der Inhaber des Bildes auf sein Urheberrecht verzichtet hat. Alamy berechnet Ihnen eine Gebühr für den Zugriff auf die hochauflösende Kopie des Bildes.

Dieses Bild kann kleinere Mängel aufweisen, da es sich um ein historisches Bild oder ein Reportagebild handel

Ähnliche Stockvideos ansehen

Stockbilder mithilfe von Tags suchen

bookcentury1900 bookdecade1900 bookpublishernewyo bookyear1901

Ähnliche Stockbilder

RM2AJGJ80–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. 160 analytische Geometrie [Ch. XII, § 86 Schnittpunkt der Tangenten an den Extremitäten chordsthrough einen festen Punkt. Diese Eigenschaft ermöglicht es uns, die polar von anypoint zu konstruieren; für eine beliebige Anzahl von Punkten auf der Polar sein kann. Abb. 87. Durch die Schnittpunkte der Tangenten bestimmt anden Enden der Akkorde durch den Punkt. 2. Die Polare des Punktes P1 in bezug auf eine centralconic ist parallel zur Tangente an der Stelle, wo der diameterthrough P1 schneidet der Kegelschnitt. Y

RM2AJGEJE–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. a-ticians waren die Trisection eines Winkels und der Verdoppelung der Cubeby Hilfe von Lineal und Zirkel allein. Es hat in letzter Zeit gezeigt, dass die Lösung dieser Probleme auf diese Weise nicht möglich ist. Beide problemsinvolve die Lösung einer kubischen Gleichung, und beide können unternommen werden, um den Bau von zwei Mean proportionals zwischen zwei straightlines zu dependupon. Dies hat auf verschiedene Art und Weise mit Hilfe von higherplane Kurven erreicht worden, und es war für diesen Zweck, dass sowohl die Conchoid andCissoid erfunden wurden. 200 analytische Geometrie [Ch. XV,

RM2AJGPG8–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. pendicu-lar zur Tangente durch den Ansprechpartner. Zum Beispiel, die Tangente an die Ellipse hat foundto b2xxx, + 2 yxy = a2 b2. Ein senkrecht zu Dieser linewill haben die Form a2yxx - b2xYy = k. Da der normalpasses durch Pv k=cfiy^^-b2 x^jv und der equationof der normalen wird a2yxx-b2 Xxy = (a2-b2) x 1 yv In der Art und Weise, wie die Gleichsetzung von der normalen thehyperbola ist ^ + ^ = ^ + ^ und der Parabel ist yxx + meine=x1yl + myv der Schüler, sollten beachten, dass diese Formeln gelten die Gleichungen der Kurven onlywhen I

RM2AJGNYA–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Abb. 72. Da die Richtung der Kurve an jedem Punkt entlang thetangent an diesem Punkt, zwei Kurven schneiden orthogonal, wenn ihre Tangenten an den Schnittpunkt perpen-dicular zu einander. Dies ist offensichtlich der Fall, weil die Tangente an die Ellipse die äusseren Winkel 136 analytische Geometrie [Kap. halbiert X, § 78 zwischen den Focal Radien, und der Tangente zur hvperbolabisects der Innenwinkel. Die Kurven daher intersectorthogonally. 4. Die Tangente an jedem Punkt einer Parabel macht equalangles mit den Focal radius

RM2AJH48M–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Dann eine einfache representingposition in einer Ebene, die durch algebraische Symbole. Dieses System iscalled die rechteckigen, und ist ein Sonderfall des Cartesiancoordinates. In der Allgemeinen kartesischen System die axesare nicht notwendigerweise senkrecht zueinander. In casethey nicht senkrecht sind, ist das System schräg genannt. Alle obigen Definitionen halten für die obliquesystem. In Abb. 8, NP ist die Abszisse von P und MP wird seinen gewöhnlichen Nate. Während die rechtwinkligen Koordinaten sind häufiger aresimpler usedbecause ihre Formeln, doch wird sie in den Lautspre- s

RM2AJGM6H–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. aufeinander bezogen, dass alle Akkorde eachbisects parallel zu den anderen. Wie diametersare sagte Konjugat in andere eacli. Die Gleichungen sind y= Lxx, und y=l2x, wo Zx und l2 angeschlossen sind, durch die die Beziehungen givenabove. In der Ellipse, Lx und l2 entgegengesetzte Vorzeichen haben, unddem Durchmesser muss durch verschiedenen Quadranten passieren. Aber in der Hyperbel, Lx und l2 das gleiche Vorzeichen haben, unddem Durchmesser müssen durch die gleichen Quadranten. Ineither Fall, wie lx sinkt in numerischer Wert, l2 erhöht, und als einer Durchmesser Ansätze der majo

RM2AJGAE6–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Koordinaten des Punkts wherethe Linie berührt die Kurve lenken, während die z-Koor- nate kann einen beliebigen Wert, was auch immer. Die Gleichung in y Xand der Kurve ist, daher ist die einzige necessaryrelation zwischen den Koordinaten eines Punkts auf der sur-Gesicht, und es wird nicht von jedem Punkt nicht auf thesurface zufrieden, ist es (wenn interpretiert als eine Gleichung in threedimensions) die Gleichung für die Oberfläche. In ähnlicher Weise, es kann gezeigt werden, dass die equationsof zylindrischen Flächen, deren Elemente parallel zur theJT-Achse enthalten sind

RM2AJH3CD–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. für alle möglichen Fälle. Es könnte seemat Erste in Abb. 12 Die Gleichung KPt=M1P1-MXKdoes nicht halten. Aber wenn MXK wird ersetzt durch die Equal-KMV die Gleichung ist auf einmal gesehen, um wahr zu sein. Lassen Sie die Schüler verschiedene Figuren zeichnen Sie mit dem pointsin verschiedenen Quadranten, und sich versichern, dass die samedemonstration gilt für alle. Es muss darauf geachtet werden, immer in der richtigen Richtung zu readthe. Für simplicitythe Zahlen werden in der Regel in den ersten Quad gebaut werden - schimpfen, aber der Schüler sollte immer befriedigen selbst Formular-barcode ist nicht restrictio

RM2AJH23X–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Er Punkt (-5, -5) an die Stelle der Abteilung. 7. Die Koordinaten der Eckpunkte eines Dreiecks sind (2, 1), (3, -2) und (-4, -1). Hier finden Sie die Gleichung der Mediane und zeigen, dass die Koordinaten des Schnittpunktes Ofany zwei Mittelpunkte der Gleichung des Dritten erfüllen, und dass die drei Mittelpunkte deshalb treffen sich in einem Punkt. 8. Was sind die Gleichungen der Diagonalen des rectanglewhose Scheitelpunkte sind (0, 0), (a, 0), (0, 6), und (a, b)? Finden thepoint Schnittpunkt, und zeigen, dass Sie zweiteilen. 9. Welches System von Leitungen ist r

RM2AJGDTJ–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. 107. Die epicycloid. - Der Weg durch einen Punkt beschrieben. Abb. 106. 204 analytische Geometrie [Ch. XV, § 108 auf der Umfang eines Kreises, die Rollen an der out-Seite von einem festen Kreis ist aufgerufen, eine epicycloid. Der Student möchte zeigen, dass die Gleichungen der Epi-zykloide sind ein+bs x - (a-b) cos(j>-b Gemütliche=("+b) sin-b Sünde, b, a+b* 108. Die Niere. - Ein wichtiger Spezialfall der theepicycloid ist die Niere, in denen a=b; aber statt

RM2AJGGJ5–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. cus auf Tangenten in der (a) (5) Ellipse, Hyperbel, Parabel (c). 6. Suchen Sie den Schauplatz der Schnittpunkt der Tangenten an theends Konjugat Durchmesser einer Ellipse. Hinweis. - Diese Lösung als ein besonderer Fall von Problem 3. 7. Suchen Sie den Schauplatz der Schnittpunkt der Tangenten an den Enden der konjugiere Durchmesser einer Hyperbel. 8. Radien vectores sind im rechten Winkel von Derschwerpunkt eine Ellipse gezeichnet. Finden der Ort der Kreuzung oftangents an den Extremitäten. 9. Finden Sie den Ort, der Mittelpunkt der Akkorde joiningthe Enden der konjugiere diamet

RM2AJGEA3–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Wert in der zweiten Gleichung und Substitution in der ersten haben wir x=a Vers-1 (-)-V2ay-y2. Aber das einzige Gleichung ist nicht so praktisch, dadie Paar Gleichungen, aus denen es gewonnen wurde, zu verwenden. Thesetwo Gleichungen, mit einer dritten Variablen, sind Equivalentto die einzige Gleichung, von denen 6 beseitigt wurde. Der Ort besteht aus einer unendlichen Anzahl von Filialen, gezeigt in Abbildung ähnlich. 103, Verlängerung sowohl Andie rechts und links von der Herkunft. 106. Die hypocycloid. - Der Weg beschrieben durch einen Punkt aufder circumferen

RM2AJGFT8–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. semicubical Parabel, und hat die Form in Abb. 1 gezeigt. 98. 105 19 G analytische Geometrie [Ch. XV, § 102 Alle Parabeln ähnlich einer dieser drei formsaccording sind auf den Wert zu n. Die student Die locusfor verschiedene Werte von n. Lassen Sie himalso zeigen, dass, wenn n eine eveninteger, oder für einen Bruchteil mit einem evennumerator und eine ungerade denomina-Tor, wird die Kurve ähnlich theordinary Parabel; wenn n eine oddinteger ist, oder für einen Bruchteil mit einem oddnumerator und eine ungerade denomina-tor, die Kurve ist ähnlich wie in Abb. 97; während, wenn n ist ein Bruchteil wit

RM2AJGT65–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. 10 Und e=3. 3. Was ist die Gleichung einer Hyperbel, wenn das Zentrum ist am Punkt (", /?) und die Achsen parallel zu den Koordinatenachsen? 4. Was ist die Gleichung der Hyperbel, die itscenter am Ursprung und seine Schwerpunkte auf der X-Achse und whichpasses durch die Punkte (5, 3) und (-3, 2)? 5. Zeigen, dass die latus Rektum der Hyperbel ist -- • 6. Zeigen, dass der Fuß des senkrecht aus dem focusof eine Hyperbel auf eine Asymptote im Abstand a von Derschwerpunkt und b vom Mittelpunkt ist. 7. Zeigen, dass der Kreis mit Radius b,

RM2AJGKBM–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. die Tangente an P2 angezeigt werden können parallel zu PVKV dieses Theorem erscheint auch aus der Tatsache, dass die tan-Herren sind besondere Fälle der System paralleler Akkorde. 6. Die Tangente am Ende der Durchmesser des parabolais parallel zum System der Akkorde, die den Durchmesser halbiert. 7. Die Fläche des Parallelogramms von Tangenten anden Enden Konjugat in Durchmessern von einem zentralen konisch geformt ist gleich thearea des Rechtecks auf die Hauptachsen. Oh. XI, § 82] Durchmesser 151 Lassen Sie ABED das Parallelogramm der tangentsat die Enden der t gebildet werden.

RM2AJGRTT–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. quilateral Hyperbel und seine konjugiere sind Evi - dank der einander gleich. Abbildung 63 zeigt ein Equi - seitliche Hyperbel und Konjugat. 118 analytische Geometrie [Ch. IX, § 70 Probleme 1. Die Gleichung einer Hyperbel Konjugat thehyperbola 4 a-2-y 2 = 4 schreiben, und ihre Achsen, Exzentrizität, latusrectum finden, die Koordinaten ihrer Schwerpunkte, und die Gleichungen der itsdirectrices. 2. Finden die Exzentrizität der Gleichseitigen Hyperbel. 3. Zeigen, dass, wenn e und e die Exzentrizität sind von zwei conju-gate Hyperbeln, - + - = 1 und Ae = werden. 4. Hier finden Sie die

RM2AJH309–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Er in - tercepts auf der X-Achse kann durch substitutingy=0 in die Gleichung gefunden werden und finden die entsprechenden Werte x; das fängt auf der y-Achse, durch Substitution von x = 0 und finden die entsprechenden Werte von y. 20. Schnittpunkt zweier Kurven. - Wenn zwei Kurven in - tersect, die Koordinaten des Schnittpunktes mustsatisfy beide Gleichungen. Um die coordinatesof einen solchen Schnittpunkt zu finden, ist es nur notwendig, um findthe Werte von x und y, die beiden Gleichungen genügen, Orin heißt, die Gleichungen zu lösen s

RM2AJGMWM–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. istangent zum Kreis beschrieben auf jedem focal Radius von theparabola als Durchmesser. 11. Die Tangente und normale an einem Punkt der Ellipse Forman gleichschenkliges Dreieck mit der X-Achse. Hier finden Sie die der Punktkoordinaten. 12. Beweisen, dass der Winkel zwischen zwei Tangenten zu einem parabolais die Hälfte der Winkel zwischen der Focal Akkorde zu thepoints Ansprechpartner. 13. Zeigen, dass die Länge eines normalen in einem equilateralhyperbola zu den Abstand der Ansprechpartner im Zentrum gleich ist. 14. Hier finden Sie die Punkte auf das konjugat Achse einer Hyperbel

RM2AJH3PF–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. entre des Dreiecks und der X-Achse passesthrough einen Scheitelpunkt? 10. Notation. - Wird es oft notwendig sein, distinguishbetween Punkte, die fest definiert sind und diejenigen, die althoughconstrained in einem bestimmten Pfad zu bewegen, dennoch kann occupyany Position auf diesem Weg. Feste Punkte werden immer durch Teilscripts, letteredPv PT usw. unterschieden und durch die Koordinaten (xv y^), (R2, t/2), etc. vertreten, während variable Punkte werden in der Regel rep werden - von der einfachen Variablen (x, y). Wenn variablepoints, deren Bewegungen sind Gover

RM2AJG6WF–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. ft, und yr werden Werte von a, m, und 7 für whichthis Ausdruck verschwindet. Dann, als, ft, und 7 approacha, ft, und 7, den Wert von p auf unbestimmte Zeit erhöht, und die Linie durch die Herkunft, deren Richtung anglesare a, m, und y kann gesagt werden, die Oberfläche atinfinity zu erfüllen. Eine solche Linie ist eine asymptotische Leitung bezeichnet. Da die Gleichung - - 1 - v -?-=0 ist die a 1 ¥ c2 nur Bedingung, die der Polar koor zufrieden sein- Dinaten der Punkte auf alle die asymptotische Zeilen, es muss die Gleichung für die asymptotische Kegel, der containsall t

RM2AJG6DD–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Abb. 20. Abb. 21. parallel zur X-F-Ebene befinden, Ellipsen, deren Achsen increaseas Abschnitt tritt zurück vom Ursprung. Sektionen byplanes parallel zu den anderen Koordinatenebenen sind parabo - Kap. V, §33] Quadric Oberflächen 255 las, die ihre Achsen parallel zur Z-Achse. Thissurface ist in Abb. 1 gezeigt. 20. Es ist eine elliptische parabo genannt -. 2 2 loid. Wenn b=#, f- & -=2 cz stellt ein paraboloid eines eine Revolution um die Z-Achse.

RM2AJGXE4–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. x + Ey + F = 0. 59. Akkord. - Wir haben gesehen, dass aus anypoint Px außerhalb des Kreises x 2 + yz = r2, zwei Tangenten können auf den Kreis gezeichnet. Lassen Sie es sein, die erforderlich sind, um die analytische Geometrie [Ch. Zu finden VII, § 59 Gleichung der Akkord P2 P3 durch 2 Punkte Contact ernennt Dieser Tangenten. Die Gleichungen der Tangenten, die P2 und P3 PX Px sind (nach [28]) und x3x+y $ = r 2. Diese beiden equationsX muss durch Auf Vi zufrieden sein) - Daher x2xx - f y 2 yx = r2 und x3 XT+ y3 y1 = r 2. Aber das sind nur die theconditions besatisfied muss, wenn die Punkte P2 ein

RM2AJGHMM–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Abb. 88. Kap. XII, § 86] Polen und POLARS 161 Lassen Sie die Koordinaten des Punktes P2 wo CP 1 Schnitte thehyperbola werden (xv ya). Dann die Gleichung der Tangente 2 k b 2 x 2 x - 2 y2 y = a2 b2, und die Gleichung der Polar von Px isb2xxx-a 2 yxy = a2 b2. Aber da Px und P2 sind auf der gleichen Leitung durch die x xorigin, - = - - und diese Zeilen sind offenbar parallel. Lassen Sie die Schüler die gleichen Theorem für die Ellipse beweisen. 3. Der Polar von jedem Punkt Px mit Bezug auf eine Parabel isparallel zur Tangente an der Stelle, an der ein Durchmesser throughP 1 schneidet die p

RM2AJGTTJ–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Auf den neuen Achsen (siehe Bild bezeichnet. 58) Ist^ + #1 = 1a2b* [36] Von der Form dieser Gleichung sehen wir, dass die Kurve issymmetrical in Bezug auf beide Achsen und damit theirintersection; dass es schneidet die X-Achse an den Punkten (±a, 0), und die W-Achse bei (0, ±b), dass die Werte von xare real nur für Werte von y Ab-b+b; und dass die Werte von Y sind real nur für Werte von x aus - ein zu-f ein. Eine sorgfältige Darstellung der Punkte showthat Es hat die Form in Abb. 1 gezeigt. 59. Die Linie DlP die Leitkurve aufgerufen wurde, und thepo

RM2AJG79P–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. ; Der Übergang von oneset von hyperbeln, die andere ein paar intersectinglines in der Ebene y=b. wm^ mmmmmmmmmmmmmmmmmmmmmmmmtmmm Abb. 17. Die Fläche ist das HYPERBOLOID von einem Blatt oder theunparted Hyperboloid genannt, die sich entlang der Z-Achse. Die Gleichungen - + - +%=1 und - r - & - + - 1 stellen eine 2 Bl< ? Ein 2 ¥ cl unparted Hyperboloide, Ausweitung der entlang der X- und der !F-axesrespectively; die Hyperboloid in jedem Fall extendingalong die Achse, deren koordinieren muss die eindeutige Zeichen in der Gleichung. Wenn a=b, die Gleichung b